Back-Door Criterion (p150)

Authors: Aymen Merrouche and Pierre-Henri Wuillemin.

This notebook follows the example from “The Book Of Why” (Pearl, 2018) chapter 4 page 150

Back-Door Criterion

import pyagrum as gum
import pyagrum.lib.notebook as gnb
import pyagrum.causal as csl
import pyagrum.causal.notebook as cslnb

In a causal diagram, confounding bias is due to the flow of non-causal information between treatment $X$ and outcome $Y$ through back-door paths. To neutralize this bias, we need to block these paths.
To block a non-causal path, we must perform an adjustment operation for a variable or a set of variables that would block the flow of information on that path. Such a set of variables satisfies what we call the “back-door” criterion. A set of variables $Z$ satisfies the back-door criterion for $(X, Y)$ if and only if:

• $Z$ blocks all back-door paths between $X$ and $Y$. A “back-door path” is any path in the causal diagram between $X$ and $Y$ starting with an arrow pointing towards $X$.
• No variable in $Z$ is a descendant of $X$ on a causal path, if we adjust for such a variable we would block a path that carries causal information hence the causal effect of $X$ on $Y$ would be biased.

If a set of $Z$ variable satisfies the back-door criterion for $(X,Y)$, the causal effect of $X$ on $Y$ is given by the formula: $P(y \mid do(x)) = \sum_{z}{P(y \mid x,z) \times P(z)}$

Example 1:

e1 = gum.fastBN("X->A->Y;A->B")
e1

m1 = csl.CausalModel(e1)
cslnb.showCausalImpact(m1, "Y", doing="X", values={})

Causal Model

$$\begin{equation*}P( Y \mid \text{do}(X)) = \sum_{A}{P\left(A\mid X\right) \cdot \left(\sum_{X'}{P\left(Y\mid A\right) \cdot P\left(X'\right)}\right)}\end{equation*}$$

Explanation : frontdoor [‘A’] found.

	Y
X	0	1
0	0.5159	0.4841
1	0.5055	0.4945

Impact

## This function returns the set of variables which satisfies the back-door criterion for (X, Y)
## None if there are no back-door paths.
setOfVars = m1.backDoor("X", "Y")
print("The set of variables which satisfies the back-door criterion for (X, Y) is :", setOfVars)

The set of variables which satisfies the back-door criterion for (X, Y) is : None

No incoming arrows into X, therefore there are no back-door paths between $X$ and $Y$ (as if we did a graph surgery according to the do operator), direct causal path $X \rightarrow A \rightarrow Y$.

Example 2:

e2 = gum.fastBN("A->B->C;A->X->E->Y;B<-D->E")
e2

m2 = csl.CausalModel(e2)
gnb.show(m2)

cslnb.showCausalImpact(m2, "Y", doing="X", values={})

Causal Model

$$\begin{equation*}P( Y \mid \text{do}(X)) = \sum_{E}{P\left(E\mid X\right) \cdot \left(\sum_{X'}{P\left(Y\mid E\right) \cdot P\left(X'\right)}\right)}\end{equation*}$$

Explanation : frontdoor [‘E’] found.

	Y
X	0	1
0	0.2473	0.7527
1	0.2099	0.7901

Impact

## This function returns the set of variables which satisfies the back-door criterion for (X, Y)
## None if there are no back-door paths.
setOfVars = m2.backDoor("X", "Y")
print("The set of variables which satisfies the back-door criterion for (X, Y) is :", setOfVars)

The set of variables which satisfies the back-door criterion for (X, Y) is : None

There is one back-door path from $X$ to $Y$ : $X \leftarrow A \rightarrow B \leftarrow D \rightarrow E \rightarrow Y$ We don’t need to control for any set of variables; this back-door path is blocked by collider node $B$ (two incoming arrows) $A \rightarrow B \leftarrow D$ Controlling for collider node $B$ would open this causal path (controlling for colliders increases bias), direct causal path $X \rightarrow E \rightarrow Y$.

Example 3:

e3 = gum.fastBN("B->X->Y;X->A<-B->Y")
e3

m3 = csl.CausalModel(e3)
cslnb.showCausalImpact(m3, "Y", doing="X", values={})

Causal Model

$$\begin{equation*}P( Y \mid \text{do}(X)) = \sum_{B}{P\left(Y\mid B,X\right) \cdot P\left(B\right)}\end{equation*}$$

Explanation : backdoor [‘B’] found.

	Y
X	0	1
0	0.6552	0.3448
1	0.1871	0.8129

Impact

## This function returns the set of variables which satisfies the back-door criterion for (X, Y)
## None if there are no back-door paths.
setOfVars = m3.backDoor("X", "Y")
print("The set of variables which satisfies the back-door criterion for (X, Y) is :", setOfVars)

The set of variables which satisfies the back-door criterion for (X, Y) is : {'B'}

There is one back-door path from $X$ to $Y$ : $Y \leftarrow B \rightarrow X$ We need to block it by controlling for $B$ wich satisfies the back-door criterion.

Example 4 (M-bias):

e4 = gum.fastBN("X<-A->B<-C->Y")
e4

m4 = csl.CausalModel(e4)
cslnb.showCausalImpact(m4, "Y", doing="X", values={})

Causal Model

$$\begin{equation*}P( Y \mid \text{do}(X)) = P\left(Y\right)\end{equation*}$$

Explanation : No causal effect of X on Y, because they are d-separated (conditioning on the observed variables if any).

Y
0	1
0.5043	0.4957

Impact

## This function returns the set of variables which satisfies the back-door criterion for (X, Y)
## None if there are no back-door paths.
setOfVars = m4.backDoor("X", "Y")
print("The set of variables which satisfies the back-door criterion for (X, Y) is :", setOfVars)

The set of variables which satisfies the back-door criterion for (X, Y) is : None

There is one back-door path from $X$ to $Y$ : $X \leftarrow A \rightarrow B \leftarrow C \rightarrow Y$ We don’t need to control for any set of variables, this back-door path is blocked by collider node $B$, the two variables are d-separated, deconfounded, independent. Controlling for collider node $B$ would make them dependant (introducing the M-bias).

Example 5:

e5 = gum.fastBN("X<-B<-A->X->Y<-C->B")
e5

m5 = csl.CausalModel(e5)
cslnb.showCausalImpact(m5, "Y", doing="X", values={})

Causal Model

$$\begin{equation*}P( Y \mid \text{do}(X)) = \sum_{C}{P\left(Y\mid C,X\right) \cdot P\left(C\right)}\end{equation*}$$

Explanation : backdoor [‘C’] found.

	Y
X	0	1
0	0.9698	0.0302
1	0.8708	0.1292

Impact

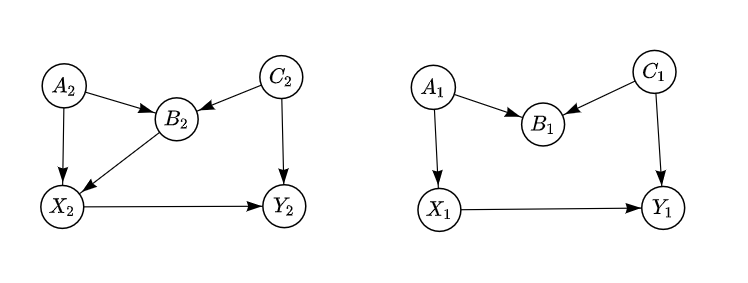
## This function returns the set of variables which satisfies the back-door criterion for (X, Y)
## None if there are no back-door paths.
setOfVars = m5.backDoor("X", "Y")
print("The set of variables which satisfies the back-door criterion for (X, Y) is :", setOfVars)

The set of variables which satisfies the back-door criterion for (X, Y) is : {'C'}

The difference between this example and the previous one is that we added an arrow between $B$ and $X$ ( $B \rightarrow X$ ), this opens a new back-door path between $X$ and $Y$ that isn’t blocked by any colliders $X \leftarrow B \leftarrow C \rightarrow Y$ We need to block the non-causal information that flows through it, controlling for $B$ closes this backdoor path (it prevents information from getting from $X$ to $C$). However, this action will open the back-door path that was formerly blocked by collider node $B$ that we are adjusting for now: $X \leftarrow A \rightarrow B \leftarrow C \rightarrow Y$ And, in this case, in addition to $B$ we would also control for $C$ or for $A$ to reblock the path we opened and to block the new path.

Another solution is to control for $C$ (it prevents information from getting from $B$ to $Y$) which satisfies the back-door criterion, it blocks the new path without reopening the one that is blocked by $B$.

Example 6:

e6 = gum.fastBN("A->X;A->B;D->A;B->X;C->B;C->E;C->Y;D->C;E->Y;E->X;F->C;F->X;F->Y;G->X;G->Y;X->Y")
e6

m6 = csl.CausalModel(e6)
cslnb.showCausalImpact(m6, "Y", doing="X", values={})

Causal Model

$$\begin{equation*}P( Y \mid \text{do}(X)) = \sum_{C,E,F,G}{P\left(Y\mid C,E,F,G,X\right) \cdot P\left(C,E,F,G\right)}\end{equation*}$$

Explanation : backdoor [‘C’, ‘E’, ‘F’, ‘G’] found.

	Y
X	0	1
0	0.6867	0.3133
1	0.5960	0.4040

Impact

## This function returns the set of variables which satisfies the back-door criterion for (X, Y)
## None if there are no back-door paths.
setOfVars = m6.backDoor("X", "Y")
print("The set of variables which satisfies the back-door criterion for (X, Y) is :", setOfVars)

The set of variables which satisfies the back-door criterion for (X, Y) is : {'F', 'C', 'G', 'E'}

Back-door paths are:

1. • $X \leftarrow G \rightarrow Y$
     
2. • $X \leftarrow E \rightarrow Y$ and any other back-door paths that go through $E$
     
3. • $X \leftarrow F \rightarrow Y$ and any other back-door paths that go through $F$
     
4. • Blocked by collider $B$ : $X \leftarrow A \rightarrow B \leftarrow C \rightarrow Y$ and any other back-door paths that go through $A$ will go through $C$
     
5. • $X \leftarrow B \leftarrow C \rightarrow Y$ and any other back-door paths that go through $B$ will go through $C$
     
     Two sets of variables that satisfy the back-door criterion are:

• {$C$,$E$,$F$,$G$} blocking (1), (2), (3) and (5)
• {$A$,$B$,$E$,$F$,$G$} blocking (1), (2), (3), (5), opening (4) and reblocking it.